HA4 Task 3 - Geometric Theory

What are the fundamental principles behind the creation of virtual 3D space? Describe and explain 3D geometry.

Remember that you are trying to comprehensively explain the theory and applications of 3D with elucidated examples and consistently using subject terminology correctly.



Geometry 

Many modeling programs do not strictly enforce geometric theory; for example, it is possible for two vertices to have two distinct edges connecting them, occupying exactly the same spatial location. It is also possible for two vertices to exist at the same spatial coordinates, or two faces to exist at the same location. Situations such as these are usually not desired and many packages support an auto-cleanup function. If auto-cleanup is not present, however, they must be deleted manually.

Cartesian Coordinates System

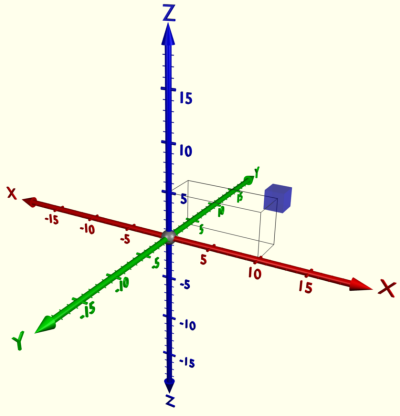
A Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length. Each reference line is called a coordinate axis or just axis of the system, and the point where they meet is its origin, usually at ordered pair (0, 0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin.

Source:http://blog.hasslberger.com/img/cartesian.png

The creator of the Cartesian Coordinates System, is by René Descartes who revolutionized mathematics by providing the first systematic link between Euclidean geometry (from the Classical Greek mathematician Euclid of Alexandria) and algebra (where letters and other general symbols are used to represent numbers and quantities in formula and equations).
Source:http://upload.wikimedia.org/wikipedia/commons/7/73/Frans_Hals_-_Portret_van_Ren%C3%A9_Descartes.jpg

Geometric Theory and Polygons

The basic object used in mesh modeling is a vertex, a point in three dimensional space. Two vertices connected by a straight line become an edge. Three vertices, connected to each other by three edges, define a triangle, which is the simplest polygon in Euclidean space. More complex polygons can be created out of multiple triangles, or as a single object with more than 3 vertices. Four sided polygons (generally referred to as quads) and triangles are the most common shapes used in polygonal modeling. A group of polygons, connected to each other by shared vertices, is generally referred to as an element. Each of the polygons making up an element is called a face.

In Euclidean geometry, any three non-collinear points determine a plane. For this reason, triangles always inhabit a single plane. This is not necessarily true of more complex polygons, however. The flat nature of triangles makes it simple to determine their surface normal, a three-dimensional vector perpendicular to the triangle's surface. Surface normal's are useful for determining light transport in ray tracing, and are a key component of the popular Phong shading model. Some rendering systems use vertex normal s instead of face normal's to create a better-looking lighting system at the cost of more processing. Note that every triangle has two face normal's, which are on the same line but opposite from each other. In many systems only one of these normal's is considered valid – the other side of the polygon is referred to as a backface, and can be made visible or invisible depending on the programmer’s desires.
Source:http://en.wikipedia.org/wiki/Geometric_primitive
Geometric Surfaces

In mathematics, specifically, in topology, a surface is a two-dimensional, topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space - for example, the surface of a ball. On the other hand, there are surfaces, such as the Klein bottle, that cannot be embedded in three-dimensional Euclidean space without introducing singularities or self-intersections.

To say that a surface is "two-dimensional" means that, about each point, there is a coordinate patch on which a two-dimensional coordinate system is defined. For example, the surface of the Earth is a two-dimensional sphere, and latitude and longitude provide two-dimensional coordinates on it.

The concept of surface finds application in physics, engineering, computer graphics, and many other disciplines, primarily in representing the surfaces of physical objects. For example, in analyzing the aerodynamic properties of an airplane, the central consideration is the flow of air along its surface.

Source:http://pushkarjoshi.org/img/JS_CAGD_2010_teaser.jpg

Primitives

The term geometric primitive in computer graphics and CAD systems is used in various senses, with the common meaning of the simplest geometric objects. A common set of two-dimensional primitives includes lines, points, and polygons, although some people prefer to consider triangles primitives, because every polygon can be constructed from triangles. All other graphic elements are built up from these primitives. In three dimensions, triangles or polygons positioned in three-dimensional space can be used as primitives to model more complex 3D forms. In some cases, curves may be considered primitives, in other cases, curves are complex forms created from many straight, primitive shapes.

Source:http://wiki.blender.org/uploads/thumb/f/f1/Mesh-primitives.png/610px-Mesh-primitives.png